On folding schemes
Zero-knowledge technology is increasingly becoming more relevant in Ethereum’s land – not only it can be used for scalability and privacy, but it also has the perfect properties for interoperability and compliance. Since PLONK came up in 2019, the paradigm for designing efficient SNARKs changed, and we have now the possibility to create proving systems that don’t rely on complicated mathematics such as bilinear pairings.
Before PLONK, most of SNARKs (eg Groth16) consisted of computing a linear PCP and combining it with pairing-based cryptography. Nowadays, modern SNARKs consist of a combination between the Polynomial IOP (or AHP) with a polynomial commitment scheme (which can be done using pairings, basic elliptic curves or hashes). It’s simple and we just have to add the Fiat-Shamir heuristic to make the process between the prover and the verifier non-interactive.
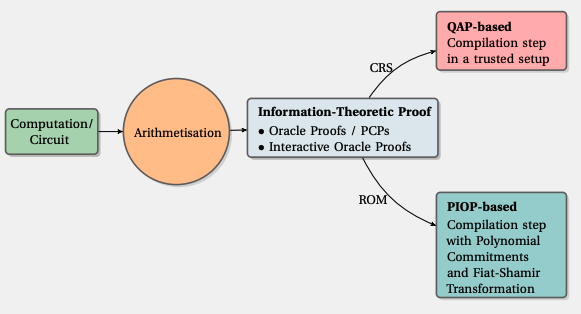
Since PLONK has a universal and updateable trusted setup, we can use it as the polynomial IOP and combine it with any given PCS – this allows the industry to use the same tooling/techniques for arithmetization and work together on improving them.
Now that we have an intuition about designing ZK proving systems (PIOP+PCS), the main goal is to achieve proofs that are more efficient – mostly, by having a smaller proof size and a faster verification time. And that’s how we get to this post’s topic: folding schemes.
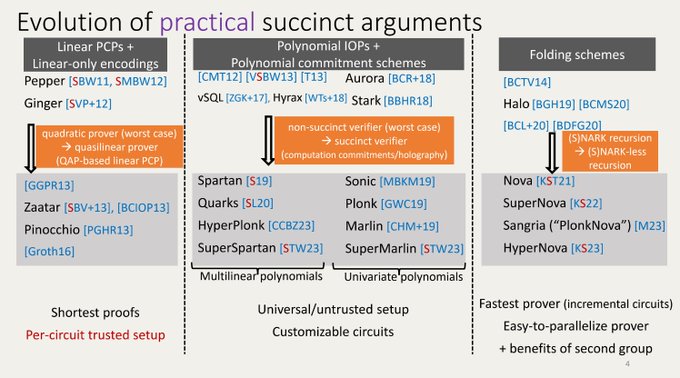
Prover time remains a bottleneck for efficient SNARKs in systems such as Groth16, PLONK and similar ones – with this in mind, Nova was invented (2021) and gave birth to “folding-scheme-based SNARKs”. In a few words, folding schemes can be seen as a pre-processing step for zkSNARKs. It’s also fair to say that, before Nova, Halo was the first practical example of recursive proof composition without a trusted setup.
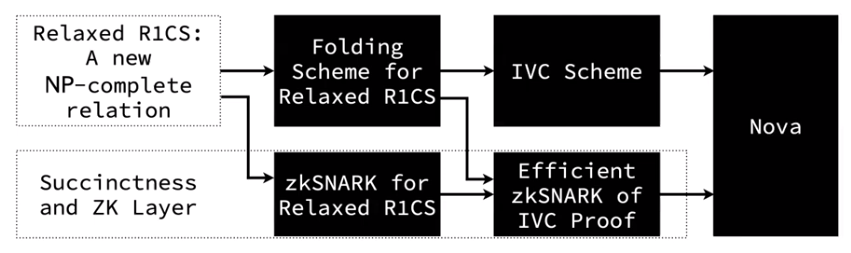
Before understanding Nova and why it’s so important, let’s take a look at another relevant concept: IVC. IVC stands for Incrementally Verifiable Computation, and it’s a term coined by Paul Valiant. Even though the paper was written in 2008, it remains important nowadays because it introduced the concept of recursive composition of proofs. IVC is a cryptographic primitive that enables a wide variety of applications including VDFs (verifiable delay functions), succinct blockchains and rollups.
The Nova paper was so relevant because it introduced a new approach to IVC. Unlike prior approaches to realize IVC, Nova introduces and employs folding schemes, a “weaker, simpler, and more efficiently realizable primitive”, which reduces the task of checking two instances in some relation to the task of checking a single instance. Finally, the Nova paper has more advantages: it doesn’t require a trusted setup nor FFTs, so it can be instantiated efficiently with any cycles of elliptic curves where the discrete logarithm is hard. Folding works with any type of elliptic curves and is expected to be 5-50x faster than previous proving systems (eg Groth16, PLONK, Halo, etc).
For more information about Nova and IVC, I recommend the reader to check this article by LambdaClass. Moreover, Dan Boneh covers efficient recursion via statement folding (including Nova, Supernova and generalizations) here, while explaining the difficulty of doing full recursion.
Ever since Nova came out in 2021, we’ve been watching an explosion of Nova related/inspired protocols. A takeway from this is that what PLONK did for zkSNARKs (with all its variants), Nova may do for ZK recursion (with all its variants as well).

While Nova was designed for a variant of R1CS (called relaxed R1CS), Sangria was designed in 2023, and it’s an efficient IVC using PLONKish arithmetization. PLONK has a more powerful arithmetization technique, which theoretically allows for even more efficient proofs than Nova.
Recursion is going to become increasingly more important, especially when we have to do proofs for very large and complicated statements because of memory constraints (eg zk-rollups).
The growth in ZK proving systems over the last decade has been absolutely insane. The Pinocchio protocol was released 10 years ago, in 2013, and nowadays, it seems we are closer and closer of achieving SNARKs with short proofs, fast proof verification and fast proof generation.